Bulk-Purchase Annuities Portfolio Construction

The bulk purchase annuity (BPA) market is bracing for record levels of transactions with over £27bn of buy-out deals reported in 2022, driven in part by rising interest rates. As insurers take on pension scheme liabilities on to their books, efficient portfolio construction becomes important for investment decision-making, ongoing management of the Matching Adjustment (MA) portfolio and competitive pricing.

In this article, we provide insight into using mathematical optimisation for optimal asset allocation given a set of constraints. The case study provided may be of relevance to new entrants to the BPA market in setting a competitive price for a BPA deal by assessing an attainable level of the MA. We expect most BPA providers to be using internal models for solvency capital requirements to fully benefit from the matching adjustment. The case study assumes that the private credit assets considered have an internal credit rating.

Investment constraints

The process of constructing a portfolio for the MA that satisfies the regulatory requirements and provides an acceptable level of risk-adjusted returns is complex. The PRA has set out three quantitative tests that must be satisfied to Ensure a well-matched asset-liability position. In addition, there are strict rules around eligibility of assets. For example, assets that are not outright eligible may need to be restructured or grouped with other assets, such as USD denominated assets being paired with cross currency swaps to qualify for the MA.

A typical MA portfolio consist of a mix of government bonds, corporate bonds, and private credit. There are usually minimum and maximum investment associated with each asset, which may exist for reasons including:

• Transaction costs may make smaller sized trades unattractive, so a minimum tradeable amount may be set.

• Investments may give rise to concentration risks, so upper limits are set to reduce exposure to a single counterparty.

• There are limits to the amount of the investment that can be originated, such as in case of commercial real estate loans or private credit assets.

A simple approach to assessing the relative attractiveness of various assets involves examining the spread on assets, with cashflows adjusted for the full fundamental spread. This spread after deductions for expected loss and cost of downgrades, represents the level of the MA on the asset. A drawback of this method is that it does not allow for considering portfolio level characteristics, such as investment limits, the PRA cashflow matching tests and other constraints that may be specific to the insurer.

In addition, the portfolio needs to be rebalanced as assets mature or new business is written, such as a BPA deal or for liquidity management. Therefore, there is an ongoing need to make investment decisions, and it is imperative that the portfolio construction method remains adaptable to accommodate such needs.

Using mathematical optimisation not only can the idiosyncrasies of the portfolio be reflected, but also a pre-trade assessment can be made of whether the proposed new investments are suitable from the investors’ perspective, such as a minimum level of risk-adjusted return.

Case Study: BPA deal

Consider an insurer that has transacted a BPA deal and has a budget/premium of 3bn to invest in a hypothetical universe of assets with different minimum and maximum investable amounts represented in the following table.

The following investment restrictions are also applicable:

• Total investment in commercial real estate loans (CREL) and infrastructure should not be less than £20m.

• The investment in gilts and corporate bonds should be at least 5% of the total investment amount.

• The total number of trades should not be less than 4 to allow for diversification.

• Optionally limiting investment in each asset to a maximum of 30% of the total amount.

To keep the example simple, we do not consider any liability characteristics but set the objective to maximise the spread on the portfolio of assets in presence of the above constraints.

Table 1: Hypothetical universe of assets

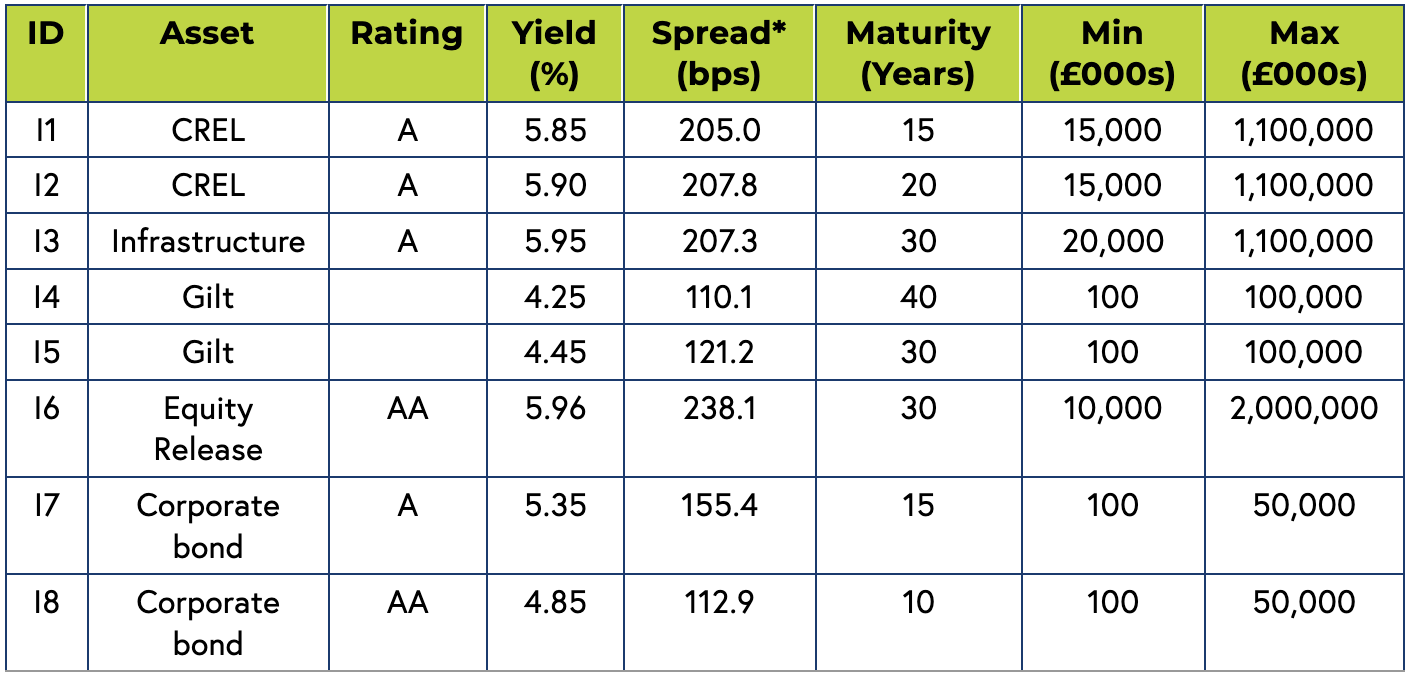
*This is Z-spread calculated using cashflows adjusted for the full fundamental spread.

Table 2: Optimisation Results

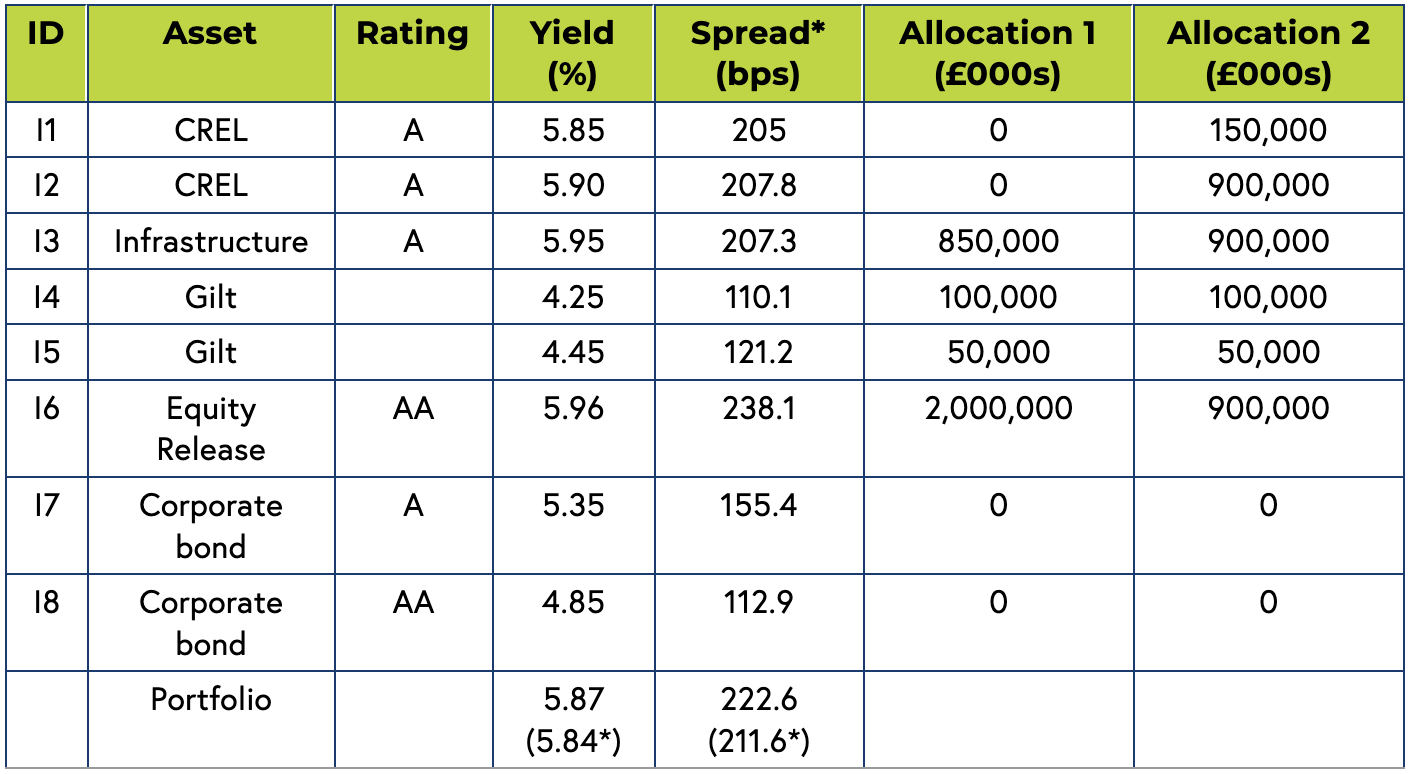
Allocation 1: Asset allocation for the case without the 30% investment restriction.
Allocation 2: Asset allocation for the case with the 30% investment restriction.
* Portfolio yield/spread for the case with the 30% investment restriction.

The optimal portfolio yield is 5.87% and spread 222.6 bps for the case without the 30% investment limit. The yield falls to 5.84% and spread to 211.6 bps when this limit kicks in as investment in higher yielding assets is reduced.

In the first case, the asset allocation is heavily concentrated in infrastructure and equity release assets, with a small allocation in gilts. This is because spreads and duration on these assets are attractive. For example, the spread on CREL (ID I2) is higher than infrastructure but duration lower, so the algorithm selects against it.

The example presented above demonstrates the construction of an optimal portfolio by employing mathematical programming to allow for various investment constraints. While the case study considered only eight assets, the method described can scale up to large portfolios consisting of thousands of lines of assets. In addition, the PRA cashflow matching tests and other portfolio management constraints can be incorporated.

Want to learn more? Contact our Head of Insurance Capital Solutions Sheikh Yasir – sheikh.yasir@4-most.co.uk.