Authors: Ramesh Indran, Sheikh Yasir, Daniel Gill and Chintan Patel
(Estimated reading time: 5 minutes)
Over the last year 4most have tested multiple approaches to optimise the hypothecation of assets to back matching adjustment eligible contracts. We have achieved real success with our algorithms improving from an initial 1% increase in matching adjustment value, to the best so far, producing a 15% increase for a UK insurer[1].
In this article we provide an insight into the challenges associated with optimising the matching adjustment and the significant reductions in capital available by applying the right approach. The difference is so marked that it is likely that insurers who do not consider sophisticated hypothecation approaches will be at a material competitive disadvantage over time.
What is the matching adjustment?
The matching adjustment is an allowance of illiquidity premium based upon the insurers assets which can be added to the risk-free interest rate term structure in the calculation of best estimate liabilities (BEL).
The matching adjustment is calculated using a methodology prescribed in the Solvency II Regulation, subject to prescribed PRA tests. The methodology and tests are designed to work such that the allowance of illiquidity premium used in the calculation of BEL is related to how well a firm’s assets and liabilities are matched.
The matching adjustment calculation methodology is effectively a derivation of the firms’ asset portfolio’s spread over risk-free, net deductions for probability of default and cost of downgrades.
For the purpose of assigning an overall matching adjustment, the portfolio of assets backing liabilities can be split/hypothecated into two components:
-
Component A: value of assets to meet probability of default; and
-
Component B: value of assets to meet cost of downgrades [2], [3].
The hypothecation of assets into these two components can have significant influence on the resulting matching adjustment value – creating an opportunity for optimisation.
Optimisation challenges
Considering the matching adjustment calculation methodology in isolation, optimisation is straightforward – the hypothecation of components A and B can be optimised to select assets which minimise the sum of probability of default and cost of downgrades; hence, maximising the matching adjustment.
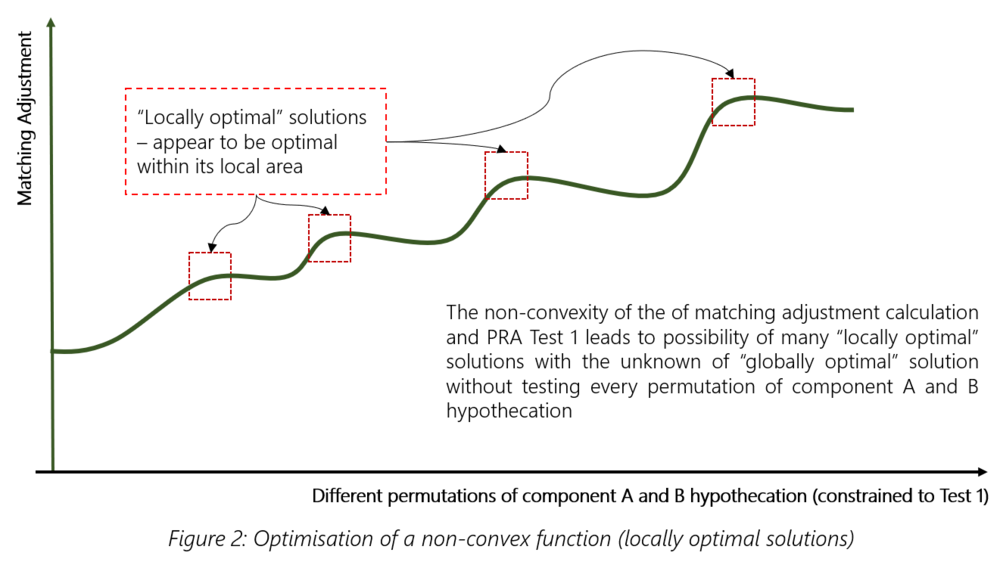
However, when considering maximising the matching adjustment whilst constrained to the PRA tests, optimisation becomes more challenging.
The three PRA prescribed tests forces firms to minimise expected accumulated cash shortfalls (Test 1); limit exposure to macroeconomic risks such as inflation, interest rates and currency (Test 2); and reduce overall cashflow mismatch (Test 3). These tests – especially Test 1 – counteract optimising component A and B of the matching adjustment calculation directly.
For example, higher illiquidity premium is generally analogous with longer duration bonds. However, longer duration income may lead to a cash shortfall when matched against expected annuity pay-outs which generally run-off with time. As such, optimisation must consider maximising the matching adjustment whilst constrained by PRA Test 1.

For non-convex functions, there could be many “locally optimal” solutions, with the “global optimal” solution being difficult to determine.
Tested approaches
We approached the optimisation challenges (counteracting features and non-convexity of features) by testing three possible optimisation techniques:
(1) Asset scoring inspired by Google’s original search return algorithms;
(2) State of the art machine learning techniques; and
(3) Non-convexity transformation approaches utilising mathematical techniques developed for network spectrum problems.

All three techniques resulted in positive increases in the matching adjustment on a like-for-like asset portfolio as the client’s current portfolio.
The asset scoring technique yielded the lowest increase at 1% and took up to three days to configure and execute. It was essentially a heuristically guided trial and error method, as such, had the main downfall of relying on judgement to overcome computing limitation of testing every possible component A and B hypothecation.
Machine learning algorithms initially proved successful showing significantly more positive results than asset scoring. However, the longer we allowed the machine learning algorithms to run, they did not fully converge. This confirmed the suspicion that machine learning algorithms could not overcome “locally optimal” pitfalls. After allowing the algorithm to run for more than a day, it netted a 5% increase in matching adjustment value.
The most successful approach we believe identified the globally optimal solution. It was produced by subtly reformulating the optimisation into a simpler convex problem. This approach resulted in 15% increase in matching adjustment executing the calculation in three seconds.
This case study has shown that an approach to matching adjustment optimisation is not necessarily one of computing power nor advanced techniques, but one that is mathematical, similar to other industries such as manufacturing which have minimised production waste whilst maximising output.
Other use-cases
Using the best approaches from a wide variety of heritages (AI, Statistical and Operations Research) we believe we can find more transparent and efficient approaches than being blinkered by any one “fashionable” style of algorithm. Additionally, there is scope to apply these techniques to wider areas related to asset-liability management.
Our next step, in the coming months, is to apply these optimisation techniques to the matching adjustment under stress for the SCR; and embedding optimisation within investment strategy or decision-making.
[1] Note: the quoted results are in the process of being baselined and may change.
[3] Note: the descriptions of component A and B are a simplification for brevity. Additionally, there are “component C” assets which are surplus for the purposes of liability coverage – component C can be ignored for optimisation purposes.
Any questions? Get in touch with Ramesh at ramesh.indran@4-most.co.uk








